这是一份manchester曼切斯特大学 MATH20401作业代写的成功案例
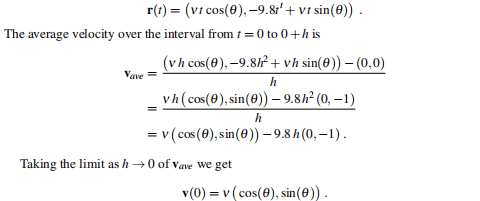
and hence
$$
\lim {n \rightarrow \infty}(n-\mu) \cdot R{A}(-(n+\mu)) \eta=\eta
$$
Therefore it follows because of
$$
\left|(n-\mu) \cdot R_{A}(-(n+\mu))\right| \leqslant \frac{c|n-\mu|}{n} \leqslant c \cdot(1+|\mu|)
$$
for every $n \in \mathbb{N}^{}$ and the denseness of $D(A)$ in $X$ that $$ s-\lim {n \rightarrow \infty}(n-\mu) \cdot R{A}(-(n+\mu))=\mathrm{id}{\mathrm{x}} . $$ Further, for every $n \in \mathbb{N}^{}$ and $\xi \in D(A)$
$$
\begin{aligned}
A{n} \xi &=(n-\mu) \cdot R_{A}(-(n+\mu))(A+n+\mu) \xi-n^{2} \cdot R_{A}(-(n+\mu)) \xi \
&=(n-\mu) \cdot R_{A}(-(n+\mu)) A \xi-\mu^{2} R_{A}(-(n+\mu)) \xi
\end{aligned}
$$

MATH20401 COURSE NOTES :
$$
\left|A \xi+c\left(\xi-A \xi_{v}\right)-c^{2} \xi_{v}\right|=\left|(A+c)\left(\xi-c \xi_{v}\right)\right| \geqslant c\left|\xi-c \xi_{v}\right|
$$
for every $v \in \mathbb{N}, c>0$ and hence that
$$
\left|\xi-\eta+c^{-1} A \xi\right| \geqslant|\xi| .
$$
Since $c$ can be chosen arbitrarily large, this leads to the contradiction
$$
\frac{1}{2}>|\xi-\eta| \geqslant|\xi|=1.4
$$