这是一份manchester曼切斯特大学 MATH20122作业代写的成功案例
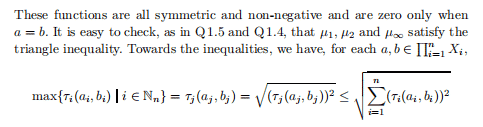
Let $k \in[0,1)$ be a Lipschitz constant for $f$. For each $a, b \in X$, we have the inequality $d(f(a), f(b)) \leq k d(a, b)$, and it follows using induction that $d\left(f^{n}(a), f^{n}(b)\right) \leq k^{n} d(a, b)$ for all $n \in \mathbb{N}$. But because $k \in[0,1), k^{n} \rightarrow 0$, so that $d\left(f^{n}(a), f^{n}(b)\right) \rightarrow 0$ also. This proves (i).
For (ii), we invoke our knowledge of real series. Suppose $x \in X$. Let $\epsilon \in \mathbb{R}^{+}$ be arbitrary. Let $m \in \mathbb{N}$ be such that $k^{m} d(x, f(x))<(1-k) \epsilon$. Then, for all
$n \in \mathbb{N}$ we have, using induction and the triangle inequality,
$d\left(f^{m}(x), f^{m+n}(x)\right) \leq k^{m} d\left(x, f^{n}(x)\right) \leq k^{m} \sum_{i=1}^{n} d\left(f^{i-1}(x), f^{i}(x)\right)$
$\leq k^{m} d(x, f(x)) \sum_{i=0}^{n-1} k^{i}$
$\leq \frac{k^{m}}{1-k} d(x, f(x))<\epsilon .$
So the ball $b\left[f^{m}(x) ; \epsilon\right)$ includes the $m$ th tail of $\left(f^{n}(x)\right)$. Since $\epsilon$ is arbitrary in $\mathbb{R}^{+}$, this establishes that $\left(f^{n}(x)\right)$ is a Cauchy sequence.

MATH20122 COURSE NOTES :
Suppose first that $P$ is complete, that $i \in \mathbb{N}{n}$ and that $\left(x{i, m}\right){m \in \mathbb{N}}$ is a Cauchy sequence in $X{i}$. For each $j \in \mathbb{N}{n} \backslash{i}$, let $a{j} \in X_{j}$. For each $m \in \mathbb{N}$, let $z_{m} \in P$ be given by $\pi_{i}\left(z_{m}\right)=x_{i, m}$ and $\pi_{j}\left(z_{m}\right)=a_{j}$ for each $j \in \mathbb{N}{n} \backslash{i}$. Then $\left(z{m}\right)$ is Cauchy in $P(6.10 .1)$ and so converges in $P(10.2 .1)$. Then $\left(\pi_{i}\left(z_{m}\right)\right)$ – that is $\left(x_{i, m}\right)$-converges in $X_{i}(6.5 .1)$. So $X_{i}$ is complete by 10.2.1. This proves the forward implication; the backward implication is easier using the same tools.