这是一份leeds利兹大学MATH262009/MATH262501作业代写的成功案例
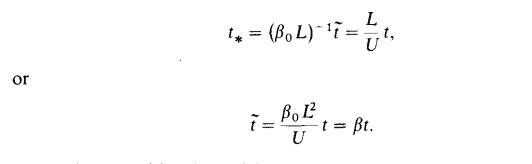

For $\beta \gg 1$ it seems logical to look for solutions in the form
$$
\begin{aligned}
\psi(x, y, \tilde{t}, \beta)=& \psi_{0}(x, y, \tilde{t})+\frac{1}{\beta} \psi_{1}(x, y, \tilde{t}) \
&+\frac{1}{\beta^{2}} \psi_{2}(x, y, \tilde{t})+\cdots
\end{aligned}
$$
whose substitution in will yield a sequence of problems for $\psi_{0}, \psi_{1}$, etc. by comparing like orders in $\beta^{-1}$. The lowest order, or $\mathrm{O}(1)$, problem for $\psi_{0}$ is
$$
\frac{\partial}{\partial t}\left(\nabla^{2} \psi_{0}-F \psi_{0}\right)+\frac{\partial \psi_{0}}{\partial x}=0,
$$
whose solution can be written as a general superposition of Rossby waves. e.g.,
$$
\psi_{0}=\sum_{j} a_{j} \cos \theta_{j},
$$
where the range of the sum over the integral index $j$ is formally infinite, but where in fact only a finite number of the amplitudes $a_{j}$ may be different from zero. The phase of each wave is
$$
\theta_{j}=k_{j} x+l_{j} y-\sigma_{j} \tilde{t}+\phi_{j},
$$

MATH262009/MATH262501 COURSE NOTES :
the solution forced by the term $a_{m} a_{n} B\left(K_{m}, K_{n}\right) \cos \left(\theta_{m}+\theta_{n}\right)$. A periodic forced solution for $\psi_{1}$ may be sought in the form
$$
\psi_{1}=A_{1 m n} \sin \left(\theta_{m}+\theta_{n}\right)
$$
where $A_{1 m n}$ is determined by $(3.26 .11 \mathrm{~b})$ to be
$$
A_{1 m n}=\frac{a_{m} a_{n} B\left(K_{m}, K_{n}\right)}{\left(K_{m n}^{2}+F\right)\left(\omega_{m n}-\sigma_{m n}\right)} .
$$