这是一份manchester曼切斯特大学 MATH36001作业代写的成功案例
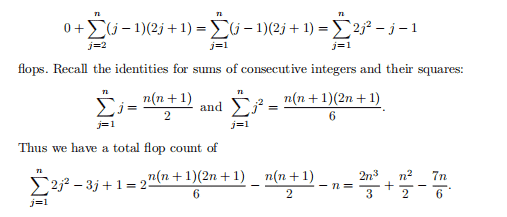

Specifically, we see from the definition of matrix multiplication that the Newton equations are equivalent to the vector equations
$$
d \mathbf{F}=J_{\mathbf{F}}\left(\mathbf{x}{0}\right) d \mathbf{x}=-\mathbf{F}\left(\mathbf{x}^{(0)}\right) $$ If the Jacobian matrix is invertible, then $$ \mathbf{x}^{(1)}-\mathbf{x}^{(0)}=J{\mathbf{F}}\left(\mathbf{x}^{(0)}\right)^{-1} \mathbf{F}\left(\mathbf{x}^{(0)}\right)
$$
whence by adding $\mathbf{x}{0}$ to both sides we see that $$ \mathbf{x}^{(1)}=\mathbf{x}^{(0)}-J{\mathbf{F}}\left(\mathbf{x}^{(0)}\right)^{-1} \mathbf{F}\left(\mathbf{x}^{(0)}\right)
$$
Now replace 1 by $n+1$ and 0 by $n$ to obtain the famous Newton formula in vector form:
$$
\mathbf{x}^{(n+1)}=\mathbf{X}^{(n)}-J_{\mathbf{F}}\left(\mathbf{X}^{(n)}\right)^{-1} \mathbf{F}\left(\mathbf{x}^{(n)}\right)
$$

MATH36001 COURSE NOTES :
Thanks to the inverse formula, we can now find an explicit formula for solving linear systems with a nonsingular coefficient matrix. Here’s how we proceed. To solve $A \mathrm{x}=\mathbf{b}$ we multiply both sides on the left by $A^{-1}$ to obtain that $\mathbf{x}=A^{-1} \mathbf{b}$. Now use the inverse formula to obtain
$$
\mathbf{x}=A^{-1} \mathbf{b}=\frac{1}{\operatorname{det} A} \operatorname{adj}(A) \mathbf{b}
$$
The explicit formula for the $i$ th coordinate of $x$ that comes from this fact is
$$
x_{i}=\frac{1}{\operatorname{det} A} \sum_{j=1}^{n} A_{j i} b_{j} .
$$