Assignment-daixieTM为您提供伯明翰大学University of Birmingham Business Analytics 07 34272 商业分析学代写代考和辅导服务!
Instructions:
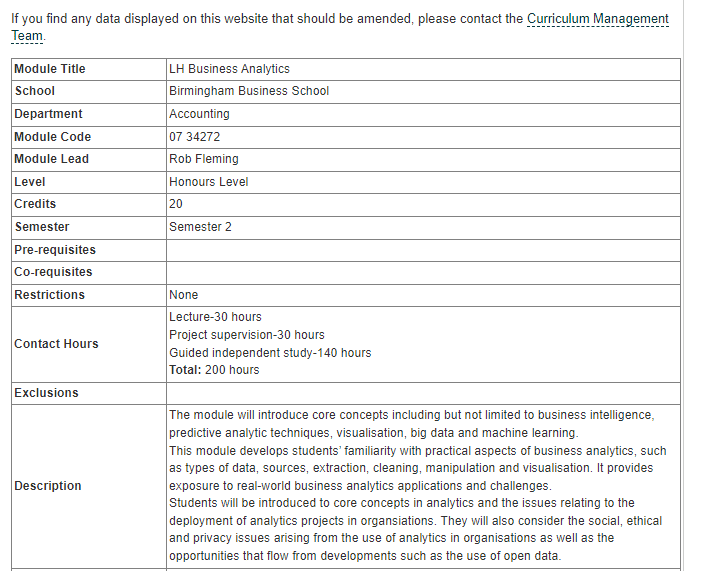
The module will provide a comprehensive overview of key concepts in business analytics, including business intelligence, predictive analytics, visualization, big data, and machine learning. Students will gain practical experience in data extraction, cleaning, manipulation, and visualization, and explore real-world applications and challenges in analytics projects.
In addition, the module will address critical issues related to the deployment of analytics projects in organizations, including social, ethical, and privacy concerns, as well as the opportunities that arise from open data initiatives. Overall, the module aims to equip students with the skills and knowledge needed to successfully navigate the rapidly evolving field of business analytics and make informed decisions about the use of analytics in organizations.
Consider a 3-period model with $t=0,1,2,3$. There are a stock and a risk-free asset. The initial stock price is $\$ 4$ and the stock price doubles with probability $2 / 3$ and drops to one-half with probability $1 / 3$ each period. The risk-free rate is $1 / 4$. (a) Compute the risk-neutral probability at each node.
To solve this problem, we can use the Cox-Ross-Rubinstein binomial tree model, which assumes that the stock price can only move up or down in each period. The risk-neutral probability $p^*$ is the probability of an up move that makes the expected return on the stock equal to the risk-free rate. Let us denote the up move by $u$ and the down move by $d$. We have:
(a) The up and down factors are given by:
$u=2, \quad d=\frac{1}{2}$
The risk-neutral probability of an up move is:
$p^*=\frac{e^{r \Delta t}-d}{u-d}=\frac{e^{(1 / 4) \cdot 1}-1 / 2}{2-1 / 2}=\frac{1}{3}$
- $q_{uu} = p^* \cdot p^* = 1/9$
- $q_{ud} = p^* \cdot (1 – p^*) = 2/9$
- $q_{du} = (1 – p^) \cdot p^ = 2/9$
- $q_{dd} = (1 – p^) \cdot (1 – p^) = 4/9$
Suppose that uncertainty in the model is described by two independent Brownian motions, $Z_{1, t}$ and $Z_{2, t}$. Assume that there exists one risky asset, paying no dividends, following the process $$ \frac{d S_t}{S_t}=\mu\left(X_t\right) d t+\sigma d Z_{1, t} $$ where $$ d X_t=-\theta X_t d t+d Z_{2, t} $$ The risk-free interest rate is constant at $r$. (a) What is the price of risk of the Brownian motion $Z_{1, t}$ ?
(a) The price of risk of the Brownian motion $Z_{1,t}$ is given by the coefficient of the stochastic differential equation for $S_t$:
$\frac{\partial S_t}{S_t}=\mu^{\prime}\left(X_t\right) d t+\sigma d Z_{1, t}$where $\mu'(X_t)$ denotes the partial derivative of $\mu(X_t)$ with respect to $X_t$. Using Itô’s lemma, we have \begin{align*} d(\log S_t)&=\frac{dS_t}{S_t}-\frac{1}{2}\frac{dS_t}{S_t}\cdot\frac{dS_t}{S_t}\ &=\mu'(X_t)dt+\sigma dZ_{1,t}-\frac{1}{2}\sigma^2 dt\ &=\left(\mu'(X_t)-\frac{1}{2}\sigma^2\right)dt+\sigma dZ_{1,t} \end{align*} Thus, the price of risk of $Z_{1,t}$ is $\gamma=\mu'(X_t)-\frac{1}{2}\sigma^2$.
(b) Give an example of a valid SPD in this model.
(b) A valid SPD for this model can be constructed using the variance-covariance matrix of the two Brownian motions. Let $V_t$ denote the vector of the two Brownian motions at time $t$, i.e. $V_t=\begin{pmatrix} Z_{1,t} \ Z_{2,t} \end{pmatrix}$. Then, the variance-covariance matrix is given by
$\Sigma=\left(\begin{array}{cc}\operatorname{Var}\left(Z_{1, t}\right) & \operatorname{Cov}\left(Z_{1, t}, Z_{2, t}\right) \ \operatorname{Cov}\left(Z_{1, t}, Z_{2, t}\right) & \operatorname{Var}\left(Z_{2, t}\right)\end{array}\right)=\left(\begin{array}{ll}1 & 0 \ 0 & 1\end{array}\right)$
since the two Brownian motions are independent and have unit variance. A valid SPD can be constructed using any positive definite matrix that is proportional to $\Sigma$. For example, we can take
$D=\left(\begin{array}{cc}\sigma_1^2 & \rho \sigma_1 \sigma_2 \ \rho \sigma_1 \sigma_2 & \sigma_2^2\end{array}\right)$
where $\sigma_1$ and $\sigma_2$ are positive constants representing the volatilities of the two Brownian motions, and $\rho$ is a constant between $-1$ and $1$ representing the correlation between the two Brownian motions. As long as $\rho^2<1$ (i.e. the correlation is not perfect), this matrix will be positive definite and therefore a valid SPD.
