如果你也在 怎样代写微分几何Differential Geometry学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。
英国论文代写Viking Essay提供最专业的一站式学术写作服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,网课代修,Exam代考等等。英国论文代写Viking Essay专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时提供查重检查,使用Turnitin高级账户查重,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
如需网课帮助,也欢迎选择英国论文代写Viking Essay!与其为国内外上课时差困扰,为国内IP无法登录zoom网课发愁,还不如选择我们高质量的网课托管服务。英国论文代写Viking Essay长期致力于留学生网课服务,涵盖各个网络学科课程:金融学Finance,经济学Economics,数学Mathematics,会计Accounting,文学Literature,艺术Arts等等。除了网课全程托管外,英国论文代写Viking Essay也可接受单独网课任务。无论遇到了什么网课困难,都能帮你完美解决!
微分几何代写Differential Geometry
微分几何学是一门研究光滑形状和光滑空间的几何学的数学学科,也被称为光滑流形。它使用微分计算、积分计算、线性代数和多线代数的技术。该领域的起源是远在古代的球面几何研究。它还与天文学、地球的大地测量学以及后来洛巴切夫斯基对双曲几何的研究有关。平滑空间最简单的例子是三维欧几里得空间中的平面和空间曲线和曲面,对这些形状的研究构成了18和19世纪现代微分几何发展的基础。
微分几何包含几个不同的主题,列举如下:
黎曼几何学Riemannian geometry代写
黎曼几何是微分几何的一个分支,研究黎曼流形,定义为具有黎曼公制的光滑流形(在每一点的切线空间上的内积,从点到点平滑变化)。这特别给出了角度、曲线长度、表面积和体积的局部概念。从这些概念中,一些其他的全局量可以通过整合局部贡献而得到。
伪黎曼尼几何学Pseudo-Riemannian geometry代写
伪黎曼几何将黎曼几何推广到公转张量不需要是正无限的情况。这种情况的一个特例是洛伦兹流形,它是爱因斯坦广义相对论引力的数学基础。
其他相关科目课程代写:
- Finsler manifold芬斯勒流形
- Symplectic geometry辛几何
微分几何的历史
微分几何作为一门学科的历史和发展,至少可以追溯到古代的古典。它与几何学、空间和形状的概念以及拓扑学,特别是流形的研究的发展密切相关。在这一节中,我们主要关注无限小方法在几何学中的应用历史,以及后来的切线空间思想,并最终在张量和张量场方面发展出该学科的现代形式主义。

The history and development of differential geometry as a discipline can be traced back at least to the ancient classics. It is closely related to the development of geometry, the concepts of space and form, and the study of topology, particularly manifolds. In this section we focus on the history of the application of infinitesimal methods to geometry, and then on the idea of tangent spaces, and finally on the development of the modern formalism of the discipline in terms of tensors and tensor fields.
微分几何相关课后作业代写
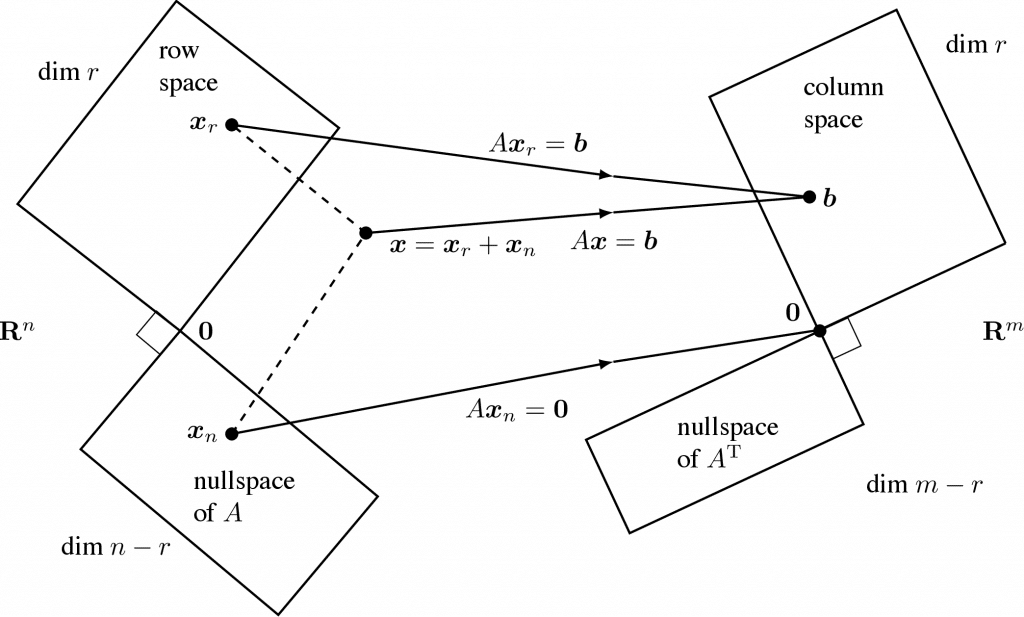
Let $c$ be a regular curve such that $|c(s)| \leq 1$ for all $s$. Suppose that there is a point $t$ where $|c(t)|=1$. Prove that the curvature at that point satisfies $|\kappa(t)| \geq 1$.
Let $c$ be a regular curve with arc length parameterization $s$. By definition, the curvature $\kappa(s)$ of the curve $c$ at the point $c(s)$ is given by $\kappa(s) = |\boldsymbol{c}”(s)|$, where $\boldsymbol{c}”(s)$ denotes the second derivative of $\boldsymbol{c}(s)$ with respect to $s$.
Since $|\boldsymbol{c}(s)| \leq 1$ for all $s$, we have $|\boldsymbol{c}'(s)| = 1$ for all $s$. Moreover, since $|\boldsymbol{c}(t)| = 1$, we have $|\boldsymbol{c}'(t)| = 0$, which implies that $\boldsymbol{c}”(t)$ is perpendicular to $\boldsymbol{c}'(t)$. Therefore, we have
$\left|\boldsymbol{c}^{\prime \prime}(t)\right|=\left|\boldsymbol{c}^{\prime \prime}(t) \cdot \frac{c^{\prime}(t)}{\left|c^{\prime}(t)\right|}\right|=\left|c^{\prime \prime}(t) \cdot \frac{c^{\prime}(t)}{\left|c^{\prime}(t)\right|}\right|$.
Now, we observe that $\boldsymbol{c}”(t) \cdot \boldsymbol{c}'(t)$ is the tangential component of $\boldsymbol{c}”(t)$ at the point $c(t)$, which is given by $\boldsymbol{c}”(t) \cdot \boldsymbol{c}'(t) = \frac{d}{ds}\left(|\boldsymbol{c}'(s)|^2\right)\bigg|{s=t} = 2|\boldsymbol{c}'(t)|\boldsymbol{c}”(t) \cdot \boldsymbol{c}'(t) = 0$. Thus, we can write $\boldsymbol{c}”(t) = \boldsymbol{c}”(t){\perp} + \boldsymbol{c}”(t){\parallel}$, where $\boldsymbol{c}”(t){\perp}$ is the perpendicular component of $\boldsymbol{c}”(t)$ to $\boldsymbol{c}'(t)$ and $\boldsymbol{c}”(t){\parallel}$ is the tangential component of $\boldsymbol{c}”(t)$ to $\boldsymbol{c}'(t)$. Since $|\boldsymbol{c}'(t)| = 0$, we have $\boldsymbol{c}”(t){\parallel} = 0$. Therefore, we have
$\left|\boldsymbol{c}^{\prime \prime}(t)\right|=\left|\boldsymbol{c}^{\prime \prime}(t){\perp}\right| \leq\left|\boldsymbol{c}^{\prime \prime}(t)\right|{\max }$
where $|\boldsymbol{c}”(t)|_{\max}$ denotes the maximum value of $|\boldsymbol{c}”(t)|$ over all vectors $\boldsymbol{v}$ perpendicular to $\boldsymbol{c}'(t)$ with $|\boldsymbol{v}| = 1$.
On the other hand, we know that the maximum value of $|\boldsymbol{c}”(t)|$ is attained when $\boldsymbol{c}
微分几何课后作业代写的应用代写
微分几何学在整个数学和自然科学领域都有应用。最突出的是,爱因斯坦在他的广义相对论中使用了微分几何的语言,随后物理学家在发展量子场理论和粒子物理学的标准模型时也使用了这种语言。在物理学之外,微分几何在化学、经济学、工程、控制理论、计算机图形和计算机视觉以及最近的机器学习中也有应用。

英国论文代写Viking Essay代写 订购流程:
第一步: 右侧扫一扫或添加WX客服mytutor01 发送代写^代考任务委托的具体要求
第二步:我们的线上客服收到您的要求后会为您匹配合适的写手,等到写手确认可以接此任务并且给出服务报价后我们将写手的报价转发给您并且收取一定的信息费,等您支付50%的定金后(有可能会向你索要更详细的作业要求)我们开始完成您交给我们的任务。
第三步: 写作完毕后发你Turnitin检测/作业完成截图(根据作业类型而定)文件,你阅读后支付余款后我们发你完整的终稿(代码,手写pdf等)
第四步: 在收到论文后,你可以提出任何修改意见,并与写手一对一讨论,我们非常愿意拉群让您和写手面对面沟通。
建议:因每份任务都具有特殊性,以上交易流程只是大概流程,更加具体的流程烦请添加客服WX免费咨询,30S通过验证,工作时间内2min回复响应,支持大多数课程的加急任务。
英国论文代写Viking Essay代写承诺&保证:
我们英国论文代写Viking Essay的政策协议保证不会将您的所有个人信息或详细信息出售或与第三方或作家共享。 相反,我们使用订单号,订单的月份和日期进行通信,并基于我们的客户与我们公司之间的现有合同,因此,即使在将来下订单时,您的身份也会在整个交易中受到保护。 我们的通信内容已通过SSL加密,以确保您以及您的论文或作业的隐私和安全性。
我们严格的写手团队要求写手“零抄袭”指导我们提供高质量的原创写作服务。 我们的业务使用Turnitin(国际版plag窃检查程序)将所有订单的剽窃报告副本发送给客户,并确保所有交付的任务都是100%原创的。 所有学术写作规则和要求,并遵循后者,包括使用参考文献和文本引用来表示和引用其他来源的内容和引语,方法是使用适当的参考样式和格式来提供高质量的服务和任务 。
我们遵守您论文的所有严格指导方针和要求,并提供至少三次修订,保证您可以拿到完全满意的论文。 仅当客户在下订单过程开始时提供详细而完整的分配说明时,此方法才有效。 我们的公司和作家在完成任务的一半或完成后不能也不会改变订单的任务。 如果作者未能找到来源,内容或未能交付的任务或任务,我们公司仅全额退款。 但是,请放心,由于我们的实时通信以及对订单交付和消费者满意度的严格规定,很少发生这种情况。英国论文代写Viking Essay 代写机构致力于打造出理科全覆盖的代写平台,所以对于很多难度很大的科目都可以提供代写服务,并且收费合理,也提供高质量的售后服务,详情咨询WX:mytutor01 作业稿件在交付之后,我们依然提供了长达30天的修改润色服务,最大程度的保证学生的代写权益。为了您的权益着想,即便最终您没有选择与我们平台合作,但依然不要去相信那些没有资历,价格低于标准的小机构,因为他们浪费的不仅仅只是你的时间和金钱,而是在变相摧毁你的学业。