Assignment-daixieTM为您提供剑桥大学University of Cambridge Marketing 3E2市场营销代写代考和辅导服务!
Instructions:
Marketing refers to the process of identifying, anticipating, and satisfying the needs and wants of consumers through the creation, promotion, distribution, and pricing of goods and services. The ultimate goal of marketing is to create value for customers and build strong relationships with them, in order to generate profitable customer actions, such as sales, repeat purchases, and brand loyalty.
Marketing involves a variety of activities, including market research, product development, branding, advertising, sales promotion, public relations, and customer service. It is a vital function of any business or organization, as it helps to connect producers with consumers, and enables businesses to effectively communicate their offerings and value propositions to their target audiences. Successful marketing strategies require a deep understanding of consumer behavior, market trends, and competitive dynamics, as well as creativity and innovation in developing and executing marketing campaigns.

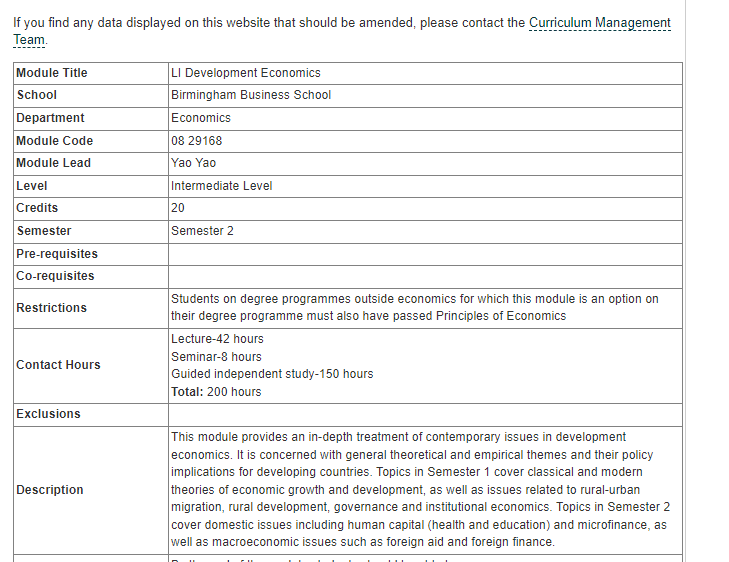
The Copper Kettle is a historic café and restaurant located on King’s Parade in Cambridge. Established more than 100 years ago, it serves drinks, breakfast, lunch and dinner every day and can also host special events. Currently they have no loyalty programme of any kind, but the General Manager is considering launching one. You have been approached to help them decide whether to go ahead with a loyalty programme or not, and how to increase customer retention. Outline your recommendations to the General Manager by addressing the following questions: (a) What are the advantage and disadvantages of loyalty programmes, and based on these, what would you recommend? Should the company launch a loyalty programme or not, and why?
(a) Loyalty programmes can offer various advantages, such as incentivizing repeat purchases, increasing customer retention and engagement, and providing valuable data and insights about customers’ preferences and behaviors. However, loyalty programmes can also be costly to implement and maintain, and there is a risk of customers signing up for the programme just for the rewards rather than being loyal to the business.
In the case of the Copper Kettle, I would recommend launching a loyalty programme. Given the highly competitive nature of the hospitality industry, offering incentives to customers can help differentiate the business and encourage them to return. Additionally, a loyalty programme can provide valuable data and insights that can inform business decisions and improve the overall customer experience. To mitigate the risk of customers joining the programme for the rewards only, the Copper Kettle can focus on creating a programme that reinforces their brand values and fosters a sense of community among customers.
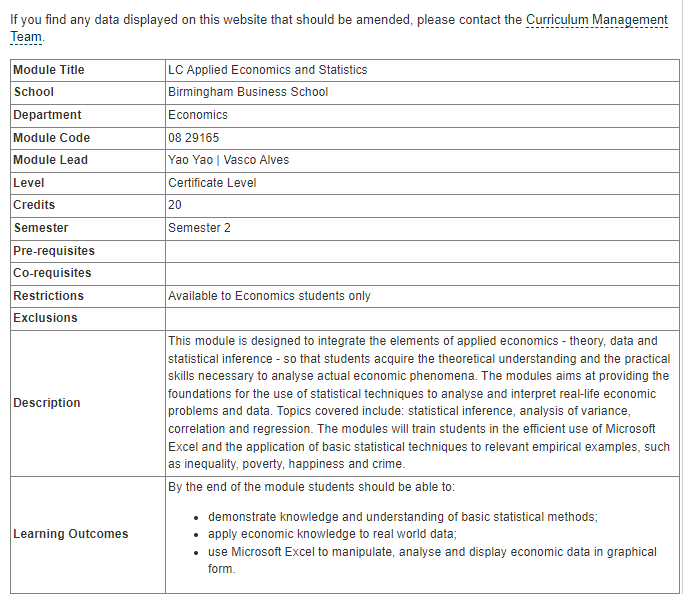
(b) Regardless of whether you think the Copper Kettle should go ahead with a formal loyalty programme or not, what would you recommend the business should do to increase its customer loyalty?
(b) Regardless of whether the Copper Kettle decides to launch a formal loyalty programme or not, there are several ways the business can increase customer loyalty. One effective approach is to focus on enhancing the overall customer experience, including personalized service, attention to detail, and a welcoming atmosphere. This can help create an emotional connection with customers and foster loyalty beyond just the incentives of a loyalty programme.
Additionally, the Copper Kettle can leverage digital marketing channels to communicate with customers and keep them engaged. This can include email newsletters, social media engagement, and targeted promotions. Providing a seamless and convenient ordering and payment process can also contribute to customer satisfaction and loyalty.
Finally, the Copper Kettle can offer special events and experiences to create unique and memorable experiences for customers. This can include wine tastings, cooking classes, and other events that align with the business’s brand and appeal to their target audience. By creating a sense of exclusivity and providing value beyond just the products and services offered, the Copper Kettle can increase customer loyalty and drive repeat business.
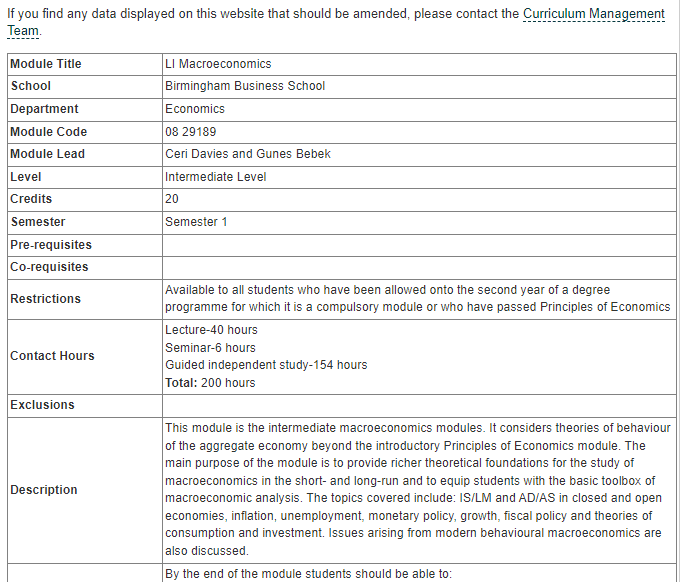
You have been approached by an entrepreneur who would like to launch a new smartphone app in the UK. The app allows users to whistle or hum a song into their phone and identifies the song for them. The entrepreneur is at the stage where she has developed a basic working version of the app, and she’s ready to launch it. She has asked you to help her with the following questions: (a) According to the product life cycle model, what should her marketing priorities be?
According to the product life cycle model, the marketing priorities for a new product like this app would depend on its current stage in the life cycle. The product life cycle has four stages: introduction, growth, maturity, and decline.
Assuming that the entrepreneur is in the introduction stage, her marketing priorities should be focused on creating awareness of the app and generating interest among potential users. This could involve creating a strong brand identity, developing a compelling value proposition, and establishing a strong social media presence to reach and engage with potential users.
Other marketing priorities at the introduction stage could include identifying and targeting early adopters who are more likely to try out new products and share their experiences with others, as well as establishing partnerships with influencers, bloggers, and other media outlets to help spread the word about the app.
Overall, the entrepreneur should focus on building a strong foundation for the app in the introduction stage, so that it can grow and mature in the subsequent stages of the product life cycle.