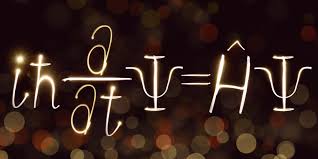这是一份bath巴斯大学PH40113作业代写的成功案

The rigorous theory of Cherenkov radiation (more correctly called Cherenkov-Vavilov radiation after its co-discoverers) was developed by Frank and Tamm from which the basic formulae are derived [6].
From this theory the emission formula is derived:
$$
\begin{array}{cc}
\mathrm{d} E / \mathrm{d} t=\left(e^{2} / c^{2}\right) & \int \sin ^{2} \theta \omega \mathrm{d} \omega . \
\text { I } & \text { II } \quad \text { III }
\end{array}
$$
The basic components of this equation were expounded by Jelley [11]. The mechanism is quite different from other, more familiar, radiation mechanisms such as synchrotron radiation or bremsstrahlung. The three factors in the Cherenkov formula for radiation yield can be understood by analogy with the single elementary classical dipole.

PH40113 COURSE NOTES :
$$
\delta u=s(\varphi) \int_{0}^{\varphi} c(\psi) q(\psi) \mathrm{d} \psi-c(\varphi) \int_{0}^{\varphi} s(\psi) q(\psi) \mathrm{d} \psi
$$
where $s(\varphi)$ and $c(\varphi)$ are two independent solutions of the homogenous equation $f_{, \rho \varphi}+(1-3 \zeta \cos \varphi) f=0$. These are the so-called Mathieu functions:
$$
s(\varphi)=\sin \varphi+O(\zeta) ; \quad c(\varphi)=\cos \varphi+O(\zeta)
$$
The O-terms are actually series in $\sin n \varphi$ or $\cos n \varphi$ of order $\zeta$ or smaller, whose explicit expression we fortunately don’t need. The whole solution is now