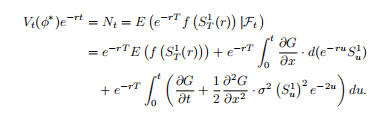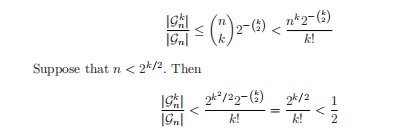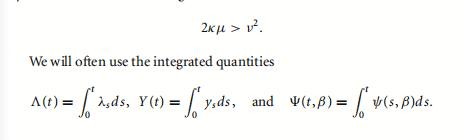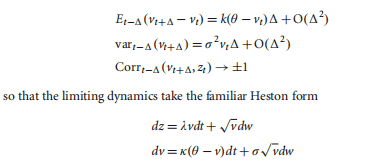The next block focuses on continuous time finance and contains an introduction to the basic ideas of Stochastic calculus. The last chapter is an overview of Actuarial Finance. This course is a great introduction to finance theory and its purpose is to give students a broad perspective on the topic.”
这是一份drps.ed爱丁堡个大学MATH10003作业代写的成功案

Once again, differentiating in $(b, c)$, we find that the random variable $\left(X_{T}, M_{T}^{X}\right)$ has the bivariate density
$$
f^{X}(T, b, c)=\frac{2(2 c-b)}{T \sqrt{T}} \phi\left(\frac{2 c-b}{\sqrt{T}}\right) \cdot e^{\mu b-\frac{1}{2} \mu^{2} T} .
$$
Note that the processes $\left(\mu t+\sigma B_{t}\right)$ and $\left(\mu t-\sigma B_{t}\right)$ have the same law. Hence we consider the process
$$
Y_{t}=\mu t+\sigma B_{t} \text { for } \sigma>0 .
$$
Write $F^{Y}(T, b, c)=P\left(Y_{T}<b, M_{T}^{Y}<c\right)$. Consider
$$
\widehat{X}{t}=\sigma^{-1} Y{t}=\frac{\mu}{\sigma} t+B_{t}
$$

MATH10003 COURSE NOTES :
Consider again the situation with two assets, the riskless bond
$$
S_{t}^{0}=e^{r t}
$$
and a risky asset $S^{1}$ with dynamics
$$
d S_{t}^{1}=S_{t}^{1}\left(\mu d t+\sigma d B_{t}\right) .
$$
$\left(B_{t}\right)$ is a standard Brownian motion on a probability space $(\Omega, \mathcal{F}, P)$. Consider the risk-neutral probability $P^{\theta}$ and the $P^{\theta}$-Brownian motion $W^{\theta}$ given by
$$
d W_{t}^{\theta}=\theta d t+\sigma d B_{t}
$$
Here $\theta=\frac{r-\mu}{\sigma}$. Under $P^{\theta}$,
$$
d S_{t}^{1}=S_{t}^{1}\left(r d t+\sigma d W_{t}^{\theta}\right),
$$