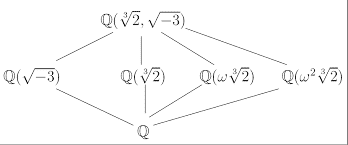
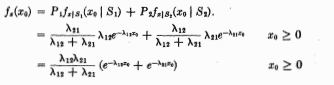To give a thorough treatment of the fundamental theory of Galois on solvability of polynomials and the subtle interplay between group theory and field theory that arises in this context.
这是一份Bath巴斯大学MA40037作业代写的成功案

Now $Q$ is a group of order $p^{n-1}$, so by the inductive hypothesis there is a sequence of subgroups $Q=Q_{0} \supset Q_{1} \supset \cdots \supset Q_{n-1}={1}$ with $Q_{i}$ a normal subgroup of $Q$ of index $p^{i}$ for each $i=1, \ldots, n-1$. Let $G_{i}=\pi^{-1}\left(Q_{i}\right)$ for $i=1, \ldots, n-1$ and $G_{n}={1}$. Then $G=G_{0} \supset G_{1} \supset \cdots \supset G_{n}={1}$ form a sequence as claimed. (Clearly $G_{i}$ has index $p^{i}$. Also, $G_{i}$ is a normal subgroup of $\mathrm{G}$ as if $g_{0} \in G_{i}$ and $g \in G$, then $g g_{0} g^{-1} \in G_{i}$ as $\pi\left(g g_{0} g^{-1}\right)=$ $\pi(g) \pi\left(g_{0}\right)(\pi(g))^{-1} \in Q_{i}$ as $Q_{i}$ is a normal subgroup of $\left.Q .\right)$

MA40037 COURSE NOTES :
By renumbering if necessary, we may assume the transposition is $\tau=$ (12).
Since $G$ acts transitively on ${1, \ldots, p}$, it has order divisible by $p$ and hence it has an element $\sigma_{0}$ of order $p$. Since $p$ is a prime, $\sigma_{0}$ is a p-cycle. Thus there is some power $\sigma=\sigma_{0}^{k}$ of $\sigma_{0}$ with $\sigma(1)=2$. By renumbering if necessary, we may then assume $\sigma=\left(\begin{array}{llll}1 & 2 & \cdots & p\end{array}\right)$. Now direct calculation shows that
$$
\sigma^{j} \tau \sigma^{-j}=(12 \cdots p)^{j}(12)(12 \cdots p)^{-j}=((j+1)(j+2))
$$
for $j=0, \ldots, p-2$. Direct calculation then shows that
$$
\begin{aligned}
(23)(12)(23) &=(13), \
(34)(13)(34) &=(14), \
\vdots & \
((p-1) p)(1(p-1))((p-1) p) &=(1 p)
\end{aligned}
$$