Tag Archives: Probability and Statistics代写

概率与统计|Probability And Statistics I4CCM141A

0
Posted on by

这是一份KCL伦敦大学 4CCM141A作业代写的成功案例

概率与统计|Probability And Statistics I4CCM141A
问题 1.


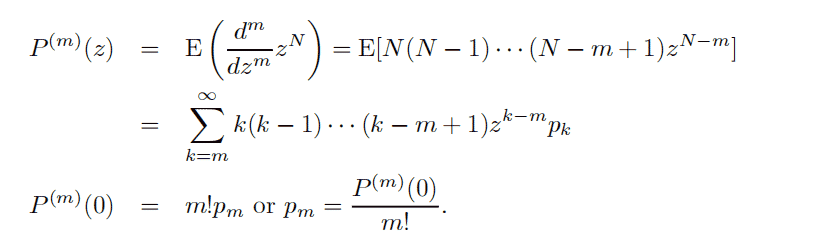
The pf for the Poisson distribution is
$$
p_{k}=\frac{e^{-\lambda} \lambda^{k}}{k !}, \quad k=0,1,2, \ldots
$$
The probability generating function from Example $3.6$ is
$$
P(z)=e^{\lambda(z-1)}, \quad \lambda>0 .
$$


证明 .

The mean and variance can be computed from the probability generating function as follows:
$$
\begin{aligned}
\mathrm{E}(N) &=P^{\prime}(1)=\lambda \
\mathrm{E}[N(N-1)] &=P^{\prime \prime}(1)=\lambda^{2} \
\operatorname{Var}(N) &=\mathrm{E}[N(N-1)]+\mathrm{E}(N)-[\mathrm{E}(N)]^{2} \
&=\lambda^{2}+\lambda-\lambda^{2} \
&=\lambda
\end{aligned}
$$

英国论文代写Viking Essay为您提供作业代写代考服务

4CCM141A COURSE NOTES ：


It is not difficult to show that the probability generating function for the negative binomial distribution is
$$
P(z)=[1-\beta(z-1)]^{-r} .
$$
From this it follows that the mean and variance of the negative binomial distribution are
$$
\mathrm{E}(N)=r \beta \text { and } \operatorname{Var}(N)=r \beta(1+\beta)
$$





概率和统计| Probability and statistics代写 MATH0057

0
Posted on by

这是一份UCL伦敦大学 MATH0057作业代写的成功案例

概率和统计| Probability and statistics代写 MATH0057
问题 1.

$$
\widehat{\eta}=\tilde{x}^{\prime} \hat{\boldsymbol{\theta}}
$$
Denoting the estimated variance of the estimates as $\widehat{\Sigma}{\theta}=\widehat{V}(\widehat{\theta})=I(\widehat{\theta})^{-1}$, then the estimated variance of the linear predictor is $$ \widehat{V}(\widehat{\eta})=\tilde{\boldsymbol{x}}^{\prime} \widehat{\boldsymbol{\Sigma}}{\theta} \tilde{\boldsymbol{x}}=\widehat{\sigma}_{\hat{\eta}}^{2}
$$


证明 .

Therefore, the $1-\alpha$ level confidence limits on $\eta$ are
$$
\left(\widehat{\eta}{\ell{1}}, \widehat{\eta}{u}\right)=\widehat{\eta} \pm Z{1-\alpha / 2} \widehat{\sigma}{\widehat{\eta}} $$


英国论文代写Viking Essay为您提供作业代写代考服务

MATH0057 COURSE NOTES ：

jth coefficient $\beta_{j}$ can be expressed as
$$
U(\theta){\beta{j}}=\sum_{i} w_{i j}\left(y_{i}-\pi_{i}\right)
$$
with weights
$$
w_{i j}=\left(\frac{1}{\pi_{i}\left(1-\pi_{i}\right)}\right) \frac{\partial \pi_{i}}{\partial \beta_{j}} .
$$





概率与统计|Probability and Statistics代写 MATH 3081

0
Posted on by

这是一份northeastern东北大学(美国)  MATH 3081作业代写的成功案

概率与统计|Probability and Statistics代写 MATH 3081
问题 1.

$$
A\left(B_{Q}\right)=\prod_{h=1}^{r} A\left(B_{q h}\right)
$$
Using these points and weights, the response model becomes
$$
z_{i j q}=x_{i j}^{\prime} \beta+z_{i j}^{\prime} T B_{q},
$$

证明 .

and so the conditional likelihood is
$$
\ell\left(\boldsymbol{Y}{i} \mid \boldsymbol{B}{q}\right)=\prod_{j=1}^{n_{i}} \Psi\left(z_{i j q}\right)^{Y_{i j}}\left[1-\Psi\left(z_{i j q}\right)\right]^{1-Y_{i j}}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

MATH 3081COURSE NOTES ：

$$
\frac{\partial \log L}{\partial \eta}=\sum_{i=1}^{N}\left[h\left(\boldsymbol{Y}{i}\right)\right]^{-1} \int{\boldsymbol{\theta}} \frac{\partial \ell_{i}}{\partial \eta} g(\boldsymbol{\theta}) d \boldsymbol{\theta}
$$
where
$$
\ell_{i}=\ell\left(\boldsymbol{Y}{i} \mid \boldsymbol{\theta}\right)=\prod{j=1}^{n_{i}} \prod_{c=1}^{C}\left(p_{i j c}\right)^{y_{i j c}}
$$
and
$$
p_{i j c}=P_{i j c}-P_{i j, c-1} .
$$