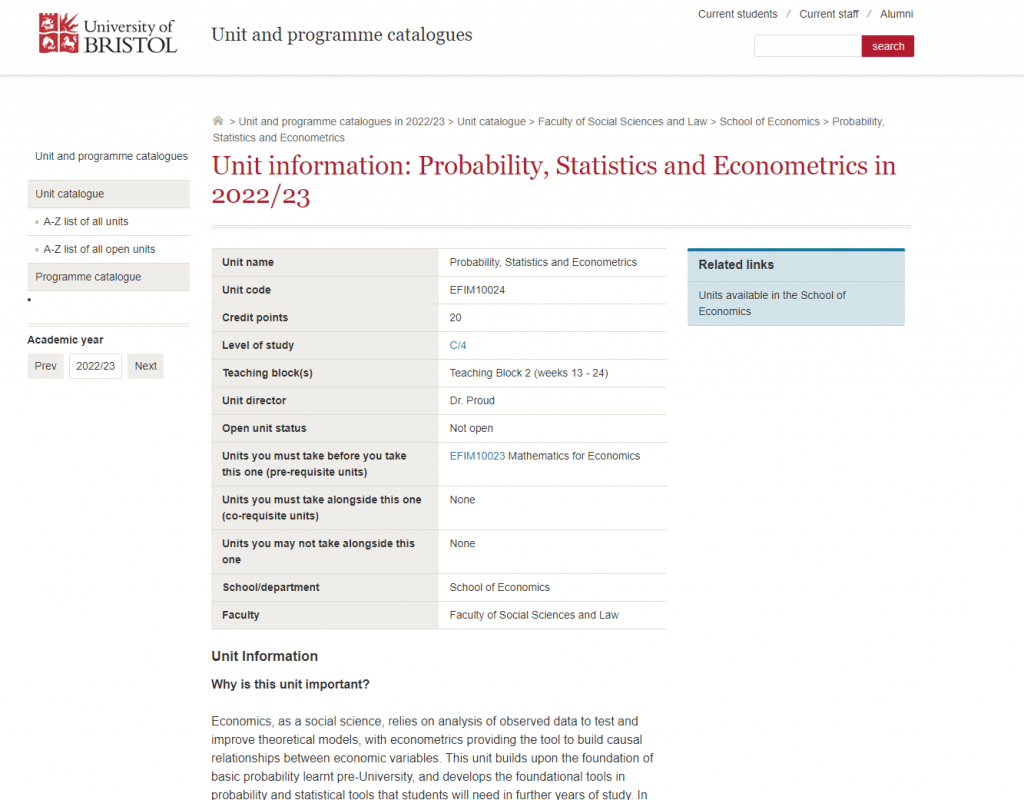
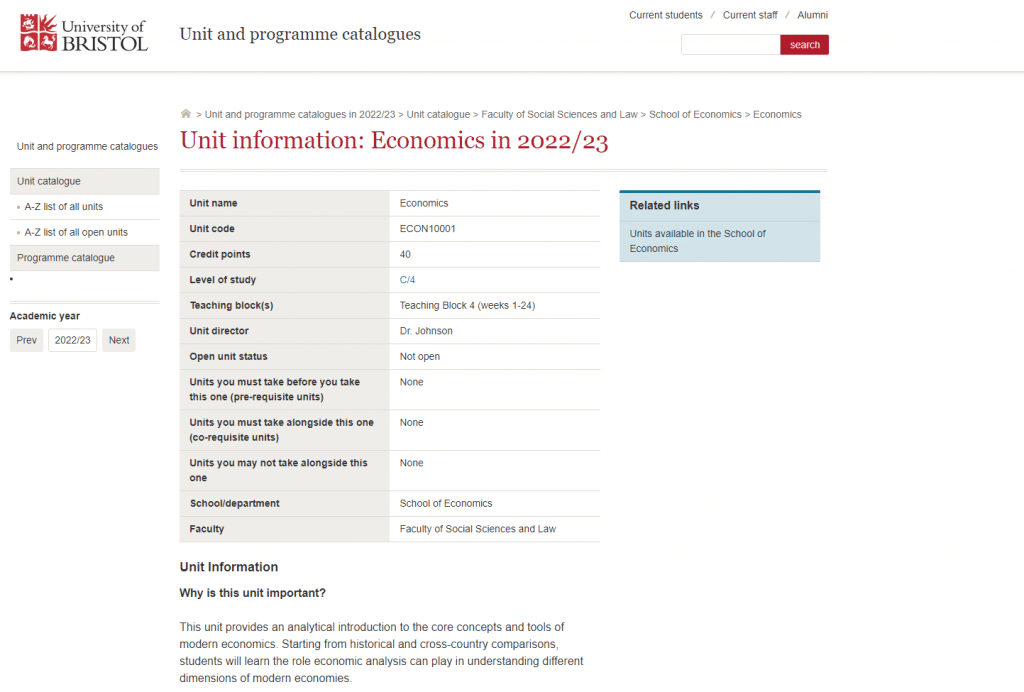
Assignment-daixieTM为您提供布里斯托大学University of Bristol Mechanics and Matter PHYS10006力学和质代写代考和辅导服务!
Instructions:
Mechanics is a branch of physics that studies the motion of objects and the forces that cause them. It is concerned with how objects move and interact with each other, and how to describe and predict these behaviors using mathematical models. Mechanics is one of the oldest and most fundamental branches of physics, and has many important applications in engineering, technology, and everyday life.
Matter is anything that has mass and takes up space. It includes all the substances that we can see and touch, as well as those that are invisible to us, such as gases and subatomic particles. Matter is made up of tiny particles called atoms, which are themselves composed of even smaller particles such as protons, neutrons, and electrons.
Mechanics and matter are closely related, since mechanics is concerned with the motion and behavior of objects, and all objects are made of matter. The behavior of matter can be described and predicted using the laws of mechanics, which tell us how objects move and interact with each other under various conditions. For example, mechanics can be used to describe the motion of a ball rolling down a hill, the behavior of a spring as it is compressed and released, or the movement of planets and stars in the universe.
In summary, mechanics and matter are two important concepts in physics that are closely related. Mechanics helps us understand how objects move and interact with each other, while matter is the substance that makes up these objects and is affected by these interactions. Together, these concepts help us to understand the behavior of the physical world around us.
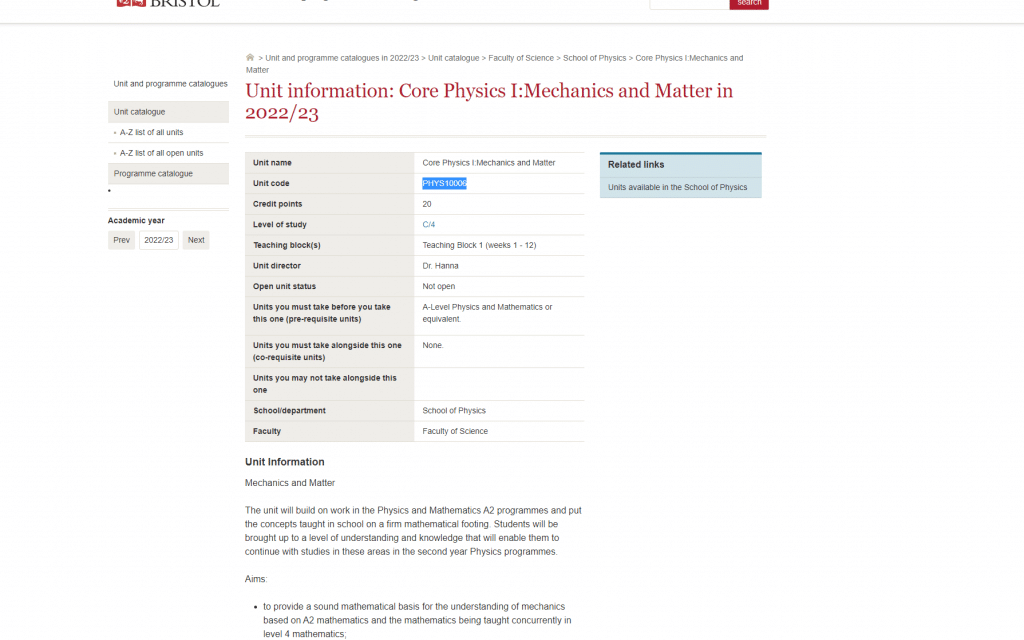
In a crash test, a truck with mass $2500 \mathrm{~kg}$ traveling at $24 \mathrm{~m} / \mathrm{s}$ smashes head-on into a concrete wall without rebounding. The front end crumples so much that the truck is $0.72 \mathrm{~m}$ shorter than before. (b) About how long does the collision last? (That is, how long is the interval between first contact with the wall and coming to a stop?)
We can use the conservation of energy to find the initial kinetic energy of the truck:
$\frac{1}{2} m v^2=\frac{1}{2}(2500 \mathrm{~kg})(24 \mathrm{~m} / \mathrm{s})^2=1.44 \times 10^6 \mathrm{~J}$
During the collision, this kinetic energy is converted into deformation work done on the truck, which we can calculate from the change in length:
$W=\frac{1}{2} k x^2=\frac{1}{2} \frac{F}{\Delta x} x^2$
where $k$ is the spring constant of the deformed truck, $x$ is the amount of deformation, and $F$ is the average force exerted by the wall on the truck. Since the truck doesn’t rebound, we can assume that all of the initial kinetic energy is converted into deformation work, so we can equate these two expressions and solve for $F$:
$1.44 \times 10^6 \mathrm{~J}=\frac{1}{2} \frac{F}{0.72 \mathrm{~m}}(0.72 \mathrm{~m})^2 \Rightarrow F=2.96 \times 10^6 \mathrm{~N}$
(c) What is the magnitude of the average force exerted by the wall on the truck during the collision?
We can use the impulse-momentum theorem to find the time interval $\Delta t$ during which the force is exerted:
$F \Delta t=\Delta p=m v_f-m v_i=2500 \mathrm{~kg}(0 \mathrm{~m} / \mathrm{s}-24 \mathrm{~m} / \mathrm{s})=-6.0 \times 10^4 \mathrm{~kg} \mathrm{~m} / \mathrm{s}$
Since the truck comes to a stop, the change in momentum is negative. Solving for $\Delta t$ gives:
$\Delta t=\frac{-6.0 \times 10^4 \mathrm{~kg} \mathrm{~m} / \mathrm{s}}{2.96 \times 10^6 \mathrm{~N}}=0.020 \mathrm{~s}$
So the collision lasts about 0.020 seconds.
It is interesting to compare this force to the weight of the truck. Calculate the ratio of the force of the wall to the gravitational force $m g$ on the truck. This large ratio shows why a collision is so damaging.
The weight of the truck is $mg = (2500 \mathrm{~kg})(9.81 \mathrm{~m/s^2}) = 24.5 \times 10^3 \mathrm{~N}$. The ratio of the force of the wall to the gravitational force on the truck is:
$\frac{2.96 \times 10^6 \mathrm{~N}}{24.5 \times 10^3 \mathrm{~N}}=120$
So the force exerted by the wall is 120 times greater than the weight of the truck. This large ratio shows why a collision can be so damaging.