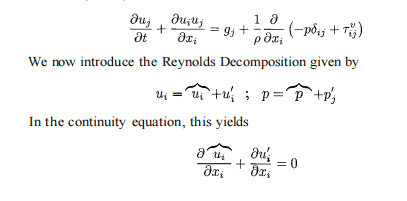财务分析 Financial Analytics BUSI70210

Posted on 2022年4月26日 by admin

这是一份 Imperial帝国理工大学 BUSI70210作业代写的成功案例

问题 1.

$$
R O I_{A}=\frac{\sum_{t=1}^{n} C F_{t}-P_{0}}{P_{0}}+n
$$
Although its concept is quite simple, this arithmetic mean return does not account for the timing of cash flows nor the compounding of investment profits. An alternative average return is the geometric mean return computed as follows:
$$
R O I_{g}=\sqrt[n]{\prod_{t=1}^{n}\left(1+r_{i}\right)}=1
$$

证明 .

where $r_{t}$ is the return on investment for a single period $t$. Another return measure which more appropriately accounts for the timing of investment cash flows is internal rate of return (IRR), which is that value for $r$ which solves the following:
$$
N P V=0=-P_{0}+\sum_{\mathrm{r}=1}^{n} \frac{C F_{t}}{(1+r)^{t}}
$$

BUSI70210 COURSE NOTES ：

$$
E[R]=\sum_{i=1}^{n} R_{i} \cdot P_{i}
$$
The statistical concept of variance is an indicator of uncertainty associated with the investment. It accounts for all potential outcomes and associated probabilities:
$$
\sigma^{2}=\sum_{i=1}^{n}\left(R_{i}-E[R]\right)^{2} P_{i}
$$
Unfortunately, in many real-world scenarios, it is very difficult to properly assign probabilities to potential outcomes. However, if we are able to claim that historical volatility indicates future variance (or, similarly, volatility or uncertainty is constant over time), we can use historical variance as our indicator of future uncertainty:
$$
\sigma_{H}^{2}=\sum_{t=1}^{n}\left(R_{t}-\bar{R}\right)^{2} \frac{1}{n}
$$

高级水动力学 Advanced Hydrodynamics PHYS97001

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS97001作业代写的成功案例

问题 1.

$$
m \Delta u=m l \frac{\partial u}{\partial y}
$$
The mass of fluid actually moving from one level $y_{0}$ to level $y_{0}+_{1}$ is proportional to $\rho\left|v^{\prime}\right|$, which leads to the expression for $\tau$
$$
\tau=m \Delta u=\rho\left|v^{\prime}\right| l \frac{\partial u}{\partial y}
$$

证明 .

For continuity reasons we must have
$$
v^{\prime} \sim u^{\prime} \sim|l| \frac{\partial u}{\partial y}
$$
This means that
$$
\tau=\rho l^{2}\left|\frac{\partial u}{\partial y}\right| \frac{\partial u}{\partial y}
$$
which expresses $\tau$ in terms of the mean flow.

PHYS97001 COURSE NOTES ：

The work done by the pressure is, per unit time
$$
p u_{i} n_{i} d S=p u_{n} d S
$$
so that the total energy flux through $d S$ is
$$
d E_{f}\left(x_{i}, t\right)=\left(p+\rho g z+\frac{1}{2} \rho u_{i} u_{i}\right) u_{n} d S
$$
and we can determine the total energy flux by integrating over the entire surface
$$
E_{f}\left(x_{i}, t\right)=\int_{S}\left(p+\rho g z+\frac{1}{2} \rho u_{i} u_{i}\right) u_{i} n_{i} d S
$$

广义相对论 General Relativity PHYS97026

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS97026作业代写的成功案例

问题 1.

Within this framework (as well as in chapter three) we need to know that $\psi_{A B C D}$ has two scalar invariants:
$$
\begin{gathered}
I \equiv \psi_{A B C D} \psi^{A B C D} \
J \equiv \psi_{A B}^{C D} \psi_{C D}^{E F} \psi_{E F} A B
\end{gathered}
$$

证明 .

Type-II space-times are such that $I^{3}=6 J^{2}$, while in type-III space-times $I=I=$
0 . Moreover, type-D space-times are characterized by the condition
$$
\psi_{P Q R\left(A \psi_{B C}\right.}^{P Q} \psi_{D E F)}^{R}=0
$$
while in type-N space-times
$$
\psi_{(A B}{ }^{E F} \psi_{C D) E F}=0
$$

PHYS97026 COURSE NOTES ：

$$
\left[\nabla^{a} \nabla^{d}+\nabla^{a} \omega^{d}-\omega^{a} \omega^{d}\right] C_{a b c d}=0
$$
We now re-express $\nabla^{a t} \omega^{d}$
$$
\nabla^{a} \omega^{d}=\omega^{a} \omega^{d}+\frac{1}{8} T g^{a d}-\frac{1}{2} R^{a d}
$$$$
\left[\nabla^{a} \nabla^{d}-\frac{1}{2} R^{a d}\right] C_{a b c d}=0
$$
This calculation only proves that the vanishing of the Bach tensor, defined as
$$
B_{b c} \equiv \nabla^{a} \nabla^{d} C_{a b c d}-\frac{1}{2} R^{a d} C_{a b e d}
$$

等离子体物理学 Plasma Physics PHYS96031

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96031作业代写的成功案例

问题 1.

note that the electric field at a location $\mathbf{x}$ due to a charge $q$ at position $\mathbf{x}{1}$ is $$ \begin{aligned} \mathbf{E}\left(\mathbf{x}, \mathbf{x}{1}\right) &=\frac{q}{4 \pi \varepsilon_{0}} \frac{\mathbf{x}-\mathbf{x}{1}}{\left|\mathbf{x}-\mathbf{x}{1}\right|^{3}} \
&=-\frac{q}{\varepsilon_{0}} \int \frac{i \mathbf{k}}{k^{2}} e^{i k \cdot\left(\mathbf{x}-\mathbf{x}_{1}\right)} \frac{d^{3} k}{(2 \pi)^{3}}
\end{aligned}
$$

证明 .

as long as the distance between $\mathbf{x}$ and $\mathbf{x}{1}$ is less than a Debye length, so negligible shielding occurs. [The validity of the Fourier transform can be demonstrated using $\left.\nabla \cdot \mathbf{E}=\left(e / \varepsilon{0}\right) \delta\left(\mathbf{x}-\mathbf{x}{1}\right)\right]$. The spatially fluctuating electric field is $$ \begin{aligned} \tilde{E}^{2} & \equiv \int n d^{3} x{1} \mathbf{E}\left(\mathbf{x}, \mathbf{x}{1}\right) \cdot \mathbf{E}\left(\mathbf{x}, \mathbf{x}{1}\right) \
&=n\left(\frac{q}{\varepsilon_{0}}\right)^{2} \int \frac{1}{k^{2}} \frac{d^{3} k}{(2 \pi)^{3}}
\end{aligned}
$$

PHYS96031 COURSE NOTES ：

If the magnetic field is toroidally symmetric, it can be written in a hybrid covariant-contravariant form using $(R, \varphi, Z)$ cylindrical coordinates,
$$
\mathbf{B}=\mu_{0} G\left(\psi_{\mathrm{p}}\right) \nabla \varphi+\nabla \varphi \times \nabla \psi_{\mathrm{p}} .
$$
The curl of this expression gives the current $\mathbf{j}=-\nabla \varphi \times$ $\nabla \mathrm{G}+\left(\Delta_{} \psi_{\mathrm{p}}\right) \nabla \varphi / \mu_{0}$ with the Grad-Shafranov operator defined by $$ \Delta_{} \psi_{\mathrm{p}} \equiv R \frac{\partial}{\partial R}\left(\frac{1}{R} \frac{\partial \psi_{\mathrm{p}}}{\partial R}\right)+\frac{\partial^{2} \psi_{\mathrm{p}}}{\partial Z^{2}} .
$$
The equilibrium equation, $\nabla p=\mathbf{j} \times \mathbf{B}$, then yields the Grad-Shafranov equation for toroidally symmetric equilibria,
$$
\nabla_{*} \psi_{\mathrm{p}}=-\mu_{0}\left(\mu_{0} G \frac{d G}{d \psi_{\mathrm{p}}}+(2 \pi R)^{2} \frac{d p}{d \psi_{\mathrm{p}}}\right) .
$$
The pressure and the poloidal current outside at constant$\psi_{p}$ surface are the natural functions for defining the equilibrium in a Grad-Shafranov solver.

激光 Lasers PHYS96023

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96023作业代写的成功案例

问题 1.

$$
T=T_{0} e^{t / T \pm z / z \mathrm{u}}
$$
and so
$$
\frac{\partial T}{\partial t}=\frac{1}{T} T
$$
and
$$
\frac{\partial^{2} T}{\partial z^{2}}=\left(\frac{1}{z_{\mathrm{D}}}\right)^{2} T
$$

证明 .

Thus
$$
\left[\left(\frac{1}{z_{\mathrm{D}}}\right)^{2}-\frac{1}{\kappa \mathrm{T}}\right] T=0,
$$
and we have a solution if
$$
z_{\mathrm{D}}=(\kappa \mathrm{T})^{1 / 2} .
$$
Therefore a characteristic distance is related to a characteristic time by $(\kappa \mathrm{T})^{1 / 2}$.
For a more realistic case consider
$$
T=T_{0} t^{-1 / 2} e^{-z^{2} / 4 x t} \quad \text { for } t>0
$$

PHYS96023 COURSE NOTES ：

has the solution
$$
T(z, t)=\left(\frac{2 \alpha I_{0}}{K}\right)(\kappa t)^{1 / 2} \operatorname{ierfc}\left[\frac{z}{2(\kappa t)^{1 / 2}}\right]
$$
where
$$
\operatorname{ierfc}(X)=\int_{X}^{\infty} \operatorname{erfc}\left(X^{\prime}\right) d X^{\prime}
$$
and
$$
\operatorname{erfc}(X)=1-\operatorname{erf}(X)=\frac{2}{\pi} \int_{X}^{\infty} e^{-\left(X^{\prime}\right)^{2}} d X^{\prime}
$$
and
$$
\operatorname{erf}(X)=\frac{2}{\pi} \int_{0}^{X} e^{-\left(X^{\prime}\right)^{2}} d X^{\prime}
$$

复杂性和网络 Complexity & Networks PHYS96008

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96008作业代写的成功案例

问题 1.

Additionally all path-specific departure rates are non-negative so we write
$$
h=\left(h_{\mathrm{p}}: p \in P\right) \geq 0
$$
where $P$ is the set of all network paths. As a consequence
$$
\Psi_{n}\left(t, h^{}\right)>v_{i i} p \in P_{i i} \Rightarrow h_{n}^{}=0 .
$$

证明 .

as can easily be proven from by contradiction. We next comment that the relevant notion of flow conservation is
$$
\sum_{p \in P_{j}} \int_{0}^{T} h_{\mathrm{p}}(t) \mathrm{d} t=Q_{i j} \quad \forall(i, j) \in W
$$
where $Q_{i j}$ is the fixed travel demand (expressed as a traffic volume) for $(i, j) \in W$. Thus, the set of feasible solutions is

PHYS96008 COURSE NOTES ：

We can then seek to work with the free energy and the model Then:
$$
F=-[N / \beta] \log Z
$$
We can also explore the standard method of calculating state functions from the free energy: ${ }^{9}$
$$
\begin{aligned}
&P=-(\partial F / \partial A){T} \ &S=-(\partial F / \partial T){A}
\end{aligned}
$$
or, using:
$$
S=-k \beta^{2}(\partial F / \partial \beta)_{A}
$$

统计力学 Statistical Mechanics PHYS96039

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96039作业代写的成功案例

问题 1.

When $X$ is a discrete random variable,
$$
\begin{aligned}
E[a X+b] &=\sum_{i}\left(a x_{i}+b\right) p\left(x_{i}\right) \
&=a \sum_{i} x_{i} p\left(x_{i}\right)+b \sum_{i} p\left(x_{i}\right) \
&=a E[X]+b
\end{aligned}
$$

证明 .

\begin{aligned}

When $X$ is a continuous random variable,
$$
\begin{aligned}
E[a X+b] &=\int_{-\infty}^{\infty}(a x+b) f(x) d x \
&=a \int_{-\infty}^{\infty} x f(x) d x+b \int_{-\infty}^{\infty} f(x) d x \
&=a E[X]+b
\end{aligned}
$$

PHYS96039 COURSE NOTES ：

$$
\sum_{j=1}^{l} a_{j}=N
$$
The total energy of the ensemble is assumed to be fixed as well. This yields our second constraint:
$$
\sum_{j=1}^{l} a_{j} e_{j}=E
$$
Let the vector $\mathbf{a}=\left(a_{1}, a_{2}, a_{3}, \cdots a_{l}\right)$ describe the occupation numbers of a system. Define $\Omega(\mathbf{a})$ to be the number of ways that the virtual systems can occupy the $l$ states. Then
$$
\Omega(\mathbf{a})=\frac{N !}{\prod_{j=1}^{l} a_{j} !}
$$

光与物质 Light & Matter PHYS96024

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96024作业代写的成功案例

问题 1.

\begin{aligned}
E_{x} &=\int \frac{k \mathrm{dq}}{r^{2}} \
&=\int_{-L / 2}^{L / 2} \frac{k \mathrm{~d} x Q}{L r^{2}} \
&=\frac{k Q}{L} \int_{-L / 2}^{L / 2} \frac{\mathrm{d} x}{(d-x)^{2}}
\end{aligned}

证明 .

\begin{aligned}
E_{x} &=\frac{k Q}{L}\left[\frac{1}{d-x}\right]_{-L / 2}^{L / 2} \
&=\frac{k Q}{L}\left(\frac{1}{d-L / 2}-\frac{1}{d+L / 2}\right) .
\end{aligned}

PHYS96024 COURSE NOTES ：

\begin{aligned}
E &=\int_{0}^{-} 2 \pi \sigma b k a\left(a^{2}+b^{2}\right)^{-3 / 2} \mathrm{~d} b \
&=2 \pi \sigma k a \int_{0} b\left(a^{2}+b^{2}\right)^{-3 / 2} \mathrm{~d} b \
&=2 \pi \sigma k a\left[-\left(a^{2}+b^{2}\right)^{-1 / 2}\right]_{b=0}^{\infty} \
&=2 \pi \sigma k
\end{aligned}

群论 Group Theory PHYS96019

Posted on 2022年4月25日 by admin

这是一份 Imperial帝国理工大学 PHYS96019作业代写的成功案例

问题 1.

$$
G=P P \cup P x_{2} P \cup \ldots \cup P x_{p} P,
$$
where $x_{1}=e$ has been omitted. Let there be $a_{g}$ left cosets of $P$ in $P x_{j} P$. We have
$$
a_{j}=\left[x_{j}^{-1} P x_{j}: x_{j}^{-1} P x_{j} \cap P\right]
$$

证明 .

$$
x_{j}^{-1} P x_{j}=\text { order } p=p^{i} \text {. }
$$
Hence $a_{j}=1$ or $p t, t \geq 1$. Now $a_{1}=1$ for the double coset $P P=P .$ Also $[G: P]=a_{1}+a_{2}+\ldots+a_{p}$. Now $p \mid[G: P]$, since $[G: P]=p^{m-i} s$, and $i \leqq(m-1)$. Thus the number of $a_{j}$ equal to 1 must be a non-zero multiple of $p$. Now $a_{j}=1$ if and only if
$$
x_{j}^{-1} P x_{j}=x_{j}^{-1} P_{x} \cap P \leftrightarrow x_{j}^{-1} P x_{j} \subset P \leftrightarrow x_{j}^{-1} P_{x}=P
$$

PHYS96019 COURSE NOTES ：

Let $H=\langle h\rangle$ and $K=\langle k\rangle$. Then
$$
[h, k]=h^{-1}\left(k^{-1} h k\right) \in H,
$$
since $H$ is normal. But also
$$
[h, k]=\left(h^{-1} k^{-1} h\right) k \in K,
$$
since $K$ is normal. Thus
$$
[h, k]=h^{-1} k^{-1} h k \in H \cap K={e} .
$$
Hence $\quad h k=k h$.
By theorem $2.8 .1$ (5),
$$
O(h k)=p q .
$$

量子力学的基础 Foundations of Quantum Mechanics PHYS96018

Posted on 2022年4月23日 by admin

这是一份 Imperial帝国理工大学 PHYS96018作业代写的成功案例

量子力学的基础 Foundations of Quantum Mechanics PHYS96018

问题 1.

To begin our analysis it is helpful to consider a simpler problem, i.e. how to solve the linear equation
$$
\frac{\mathrm{d} \varphi}{\mathrm{d} t}=A \varphi
$$
on a finite-dimensional vector space $V$. If the matrix $A$ is diagonalizable and all eigenvalues are simple (i.e. without degeneracy), the space $V$ has a basis of right eigenvectors $\left{v_{j}\right}$ :
$$
A v_{j}=\varepsilon_{j} v_{j}
$$

证明 .

$$
\varphi(0)=\sum_{k=1}^{N} B_{k} v_{k},
$$
where the coefficients of linear combination are obtained by using the left eigenvectors $v^{j}$ satisfying
$$
v^{j} A=\varepsilon_{j} v^{j}
$$
in the form
$$
B_{j}=\left(v^{j}, \varphi(0)\right)
$$

PHYS96018 COURSE NOTES ：

The operator of the electric dipole moment reads $d=-e x$, or, upon transformation to a spherical basis, defined by $d_{\pm 1}=\mp\left(d_{1} \pm i d_{2}\right) / \sqrt{2}$, $d_{0}=d_{3}$,
$d_{\mu}=-e \sqrt{\frac{4 \pi}{3}} r Y_{1 \mu} .$
Converting the field $\boldsymbol{E}$ to the same basis,
$$
E_{+1}=-\frac{1}{\sqrt{2}}\left(E_{1}+\mathrm{i} E_{2}\right), \quad E_{-1}=\frac{1}{\sqrt{2}}\left(E_{1}-\mathrm{i} E_{2}\right), \quad E_{0}=E_{3},
$$
the scalar product becomes
$$
\boldsymbol{d} \cdot \boldsymbol{E}=\sum_{\mu} d_{\mu}^{} E_{\mu}=\sum_{v} d_{v} E_{v}^{} .
$$

英国论文代写Viking Essay

Top50phd导师团队，专注于英国论文代写7年

Tag Archives: imperial代写

财务分析 Financial Analytics BUSI70210

BUSI70210 COURSE NOTES ：

高级水动力学 Advanced Hydrodynamics PHYS97001

PHYS97001 COURSE NOTES ：

广义相对论 General Relativity PHYS97026

PHYS97026 COURSE NOTES ：

等离子体物理学 Plasma Physics PHYS96031

PHYS96031 COURSE NOTES ：

激光 Lasers PHYS96023

PHYS96023 COURSE NOTES ：

复杂性和网络 Complexity & Networks PHYS96008

PHYS96008 COURSE NOTES ：

统计力学 Statistical Mechanics PHYS96039

PHYS96039 COURSE NOTES ：

光与物质 Light & Matter PHYS96024

PHYS96024 COURSE NOTES ：

量子力学的基础 Foundations of Quantum Mechanics PHYS96018

PHYS96018 COURSE NOTES ：