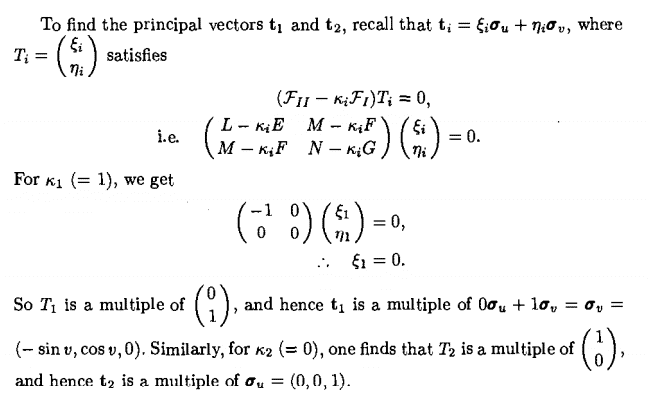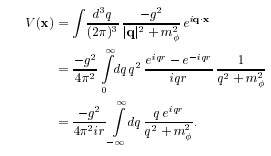Tag Archives: KCL代写

群与对称性|Groups And Symmetries代写  5CCM232A

0
Posted on by

这是一份kcl伦敦大学学院 5CCM232A作业代写的成功案

群与对称性|Groups And Symmetries代写  5CCM232A
问题 1.

Thus
$$
\sum_{g \in S}\left|G_{g}\right|=\sum_{g \in G}|F(g)| .
$$
Let $s_{1}, s_{2}, s_{3}, \cdots g^{s_{t}}$ be representatives of the $t$ orbits $(1 .$ e. we take just one $s_{i}$ from each orbit). Then
$$
\sum_{i=1}^{t} \sum_{s \in G\left(s_{i}\right)}\left|G_{s}\right|=\sum_{g \in G}|F(g)| .
$$
By theorem, if $s \in G\left(s_{i}\right)$, then
$$
G_{s_{i}}=g G_{g} g^{-1},
$$
where $g(s)=s_{i}$. Thus

证明 .

$$
\left|G_{b_{i}}\right|=\left|G_{g}\right|,
$$
when $\varepsilon \in G\left(s_{i}\right)$. Hence
$$
\sum_{i=l}^{t}\left|G\left(s_{i}\right)\right|\left|G_{s_{i}}\right|=\sum_{g \in G}|F(g)| .
$$
By theorein $4.6 .3$ (4),
$$
\left|G\left(s_{i}\right)\right|\left|a_{g_{i}}\right|=|G| .
$$
Hence finally
$$
t|G|=\sum_{g \in G} F(g) .
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

5CCM232A COURSE NOTES ：

Note that
$$
\bar{g}^{r}=\overline{\left(g^{r}\right)}=g^{r} Z(G) .
$$
Th1s means that $G$ consists of the cosets
$$
g Z(G), \quad g^{2} Z(G), \quad g^{3} Z(G), \ldots, g^{p-1} Z(G), \quad g^{P} Z(G)=Z(G) .
$$
Thus
$$
G=g Z(G) \cup g^{2} Z(G) \cup \ldots U g^{p-1} 2(G) \cup 2(G)
$$
Now let $x, y$ be any two elements of $G$. Then
$$
\text { and } \quad x \in g^{i} Z(G)
$$




平面几何学|Geometry Of Surfaces代写  5CCM223A

0
Posted on by

这是一份kcl伦敦大学学院  5CCM223A作业代写的成功案

平面几何学|Geometry Of Surfaces代写  5CCM223A
问题 1.

so we get
$$
H=\frac{1}{2}\left(\frac{\dot{g}}{f}-\frac{\ddot{f}}{\dot{g}}\right)
$$
Since $\dot{g}^{2}=1-\dot{f}^{2}, \mathcal{S}$ is minimal if and only if
$$
f \ddot{f}=1-\dot{f}^{2} .
$$

证明 .

To solve the differential equation (8), put $h=\dot{f}$, and note that
$$
\ddot{f}=\frac{d h}{d t}=\frac{d h}{d f} \frac{d f}{d t}=h \frac{d h}{d f} .
$$
Hence, Eq. (8) becomes
$$
f h \frac{d h}{d f}=1-h^{2}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

5CCM223A COURSE NOTES ：

$$
\iint_{\mathcal{S}} K d \mathcal{A}=0 \text {. }
$$
Can such a surface have $K=0$ everywhere?
Show that, if $\mathcal{S}$ is the ellipsoid
$$
\frac{x^{2}+y^{2}}{a^{2}}+\frac{z^{2}}{b^{2}}=1,
$$
where $a$ and $b$ are positive constants,
$$
\iint_{\mathcal{S}} K d \mathcal{A}=4 \pi \text {. }
$$




几何拓扑学|Geometric Topology代写 6CCM327A

0
Posted on by

这是一份kcl伦敦大学学院 6CCM326A作业代写的成功案

几何拓扑学|Geometric Topology代写 6CCM327A
问题 1.

PROOF: Using obstruction theory one sees there is a unique extension $f$ in
$$
\text { localization } \times \text { identity } Y \times Y^{\prime}
$$

证明 .

Thus we have natural maps
$$
\widehat{X}{S} \rightarrow X{A}
$$
which imply a map
$$
\underset{\vec{s}}{\lim } \widehat{X}{S} \stackrel{A}{\rightarrow} X{A}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

6CCM327A COURSE NOTES ：

$$
\text { image }\left(\pi_{k} X_{n-1} \rightarrow \pi_{k} Y_{n-1}\right)
$$
Then $a^{\prime}$ works for the new localization
$$
S^{k} \rightarrow S_{0}^{k} \stackrel{m}{\cong} S_{0}^{k}
$$
and $X_{n}=X_{n-1} / S^{k} \cong$ cofibre $a^{\prime}$ satisfies
$$
\left(X_{n}\right){0} \cong Y{n} .
$$




广义理论和重正化|Gauge Theory and Renormalisation代写 7CCMMS43

0
Posted on by

这是一份kcl伦敦大学学院 6CCM326A作业代写的成功案例

广义理论和重正化|Gauge Theory and Renormalisation代写 7CCMMS43
问题 1.

$$

The second factor in is
$$
\begin{aligned}
\int_{0}^{\infty} d \ell \frac{\ell^{d-1}}{\left(\ell^{2}+\Delta\right)^{2}} &=\frac{1}{2} \int_{0}^{\infty} d\left(\ell^{2}\right) \frac{\left(\ell^{2}\right)^{\frac{d}{2}-1}}{\left(\ell^{2}+\Delta\right)^{2}} \
&=\frac{1}{2}\left(\frac{1}{\Delta}\right)^{2-\frac{d}{2}} \int_{0}^{1} d x x^{1-\frac{d}{2}}(1-x)^{\frac{d}{2}-1}
\end{aligned}
$$

证明 .

where we have substituted $x=\Delta /\left(\ell^{2}+\Delta\right)$ in the second line. Using the definition of the beta function,
$$
\int^{1} d x x^{\alpha-1}(1-x)^{\beta-1}=B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

7CCMMS43 COURSE NOTES ：

Then we can write the currents associated with these symmetries as
$$
\begin{gathered}
j_{L}^{\mu}=\bar{Q}{L} \gamma^{\mu} Q{L}, \quad j_{R}^{\mu}=\bar{Q}{R} \gamma^{\mu} Q{R}, \
j_{L}^{\mu a}=\bar{Q}{L} \gamma^{\mu} \tau^{a} Q{L}, \quad j_{R}^{\mu a}=\bar{Q}{R} \gamma^{\mu} \tau^{a} Q{R},
\end{gathered}
$$
where $\tau^{a}=\sigma^{a} / 2$ represent the generators of $S U(2)$. The sums of left- and right-handed currents give the baryon number and isospin currents
$$
j^{\mu}=\bar{Q} \gamma^{\mu} Q, \quad j^{\mu a}=\bar{Q} \gamma^{\mu} \tau^{\alpha} Q
$$




伽罗瓦理论|Galois Theory代写6CCM326A

0
Posted on by

这是一份kcl伦敦大学学院 6CCM326A作业代写的成功案

伽罗瓦理论|Galois Theory代写6CCM326A
问题 1.

$$
b^{\prime}=a^{\prime} \sum_{i=1}^{p-1} \zeta^{i}=((p-3) / 4) \sum_{i=1}^{p-1} \zeta^{i}=((p-3) / 4)(-1)=-(p-3) / 4
$$
and then
$$
b=(p-1) / 2+b^{\prime}=(p-1) / 2-(p-3) / 4=(p+1) / 4
$$

证明 .

Now
$$
\begin{aligned}
\left(X-\alpha_{0}\right)\left(X-\alpha_{1}\right) &=X^{2}-\left(\alpha_{0}+\alpha_{1}\right) X+\alpha_{0} \alpha_{1} \
&=X^{2}+X+b,
\end{aligned}
$$
so
$$
\begin{array}{ll}
\left(X-\alpha_{0}\right)\left(X-\alpha_{1}\right)=X^{2}+X-(p-1) / 4 & \text { if } p \equiv 1(\bmod 4) \
\left(X-\alpha_{0}\right)\left(X-\alpha_{1}\right)=X^{2}+X+(p+1) / 4 & \text { if } p \equiv 3(\bmod 4)
\end{array}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

6CCM326ACOURSE NOTES ：

$$
\theta=\alpha_{1} Y_{1}+\cdots+\alpha_{n} Y_{n} \in \tilde{\mathbf{E}}
$$
and let
$$
F(Z)=\prod_{\tau^{\prime} \in S_{n}}\left(Z-\tau^{\prime}(\theta)\right) \in \tilde{\mathbf{E}}[Z]
$$
The polynomial $F(Z)$ is a symmetric function of its roots, so by Lemma its coefficients are functions of the elementary symmetric functions of its roots and hence of $Y_{1}, \ldots, Y_{n}$ and the coefficients of $f(X)$. Thus, $F(Z) \in$ $\tilde{\mathbf{F}}[Z]$. Now we may factor $F(Z)$ into a product of irreducibles in $\tilde{\mathbf{F}}[Z]$,
$$
F(Z)=F_{1}(Z) \cdots F_{t}(Z)
$$




概率论的基本原理|Fundamentals of Probability Theory代写 6CCM341A

0
Posted on by

这是一份kcl伦敦大学学院  6CCM341A作业代写的成功案

概率论的基本原理|Fundamentals of Probability Theory代写 6CCM341A
问题 1.

Note that for any random variable $y$, defined by $y=a r+b$, we may obtain $f_{v}^{T}(s)$ in terms of $f_{r}^{T}(s)$ from the definition of the $s$ transform as. follows:
$f_{\nu}{ }^{T}(s)=E\left(e^{-w}\right)=E\left(e^{-a-s^{-s} e^{-\infty}}\right)=e^{-\Delta t} \int_{-\infty}^{n} e^{-\operatorname{anv} f_{r}\left(r_{0}\right) d r_{0}}$
We may recognize the integral in the above equation to obtain $f_{y}^{T}(s)=e^{-\Delta b_{p}}{ }^{T}(a s)$


证明 .

We shall apply this relation to the ease where $y$ is the standardized random variable for $r$,
$$
y=\frac{r-E(r)}{\sigma_{p}}=\frac{r-n E(x)}{\sqrt{n} \sigma_{n}} \quad a=\frac{1}{\sqrt{n} \sigma_{s}} \quad b=-\frac{\sqrt{n} E(x)}{\sigma_{z}}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

6CCM341A COURSE NOTES ：

and if $a$ and $b$ are integers with $b>a$, there follows
$\operatorname{Prob}(a \leq k \leq b)=\sum_{k_{0}=a}^{b}\left(\begin{array}{l}n \ k_{0}\end{array}\right) P v_{k}(1-P)^{a-k_{0}}$
Should this quantity be of interest, it would generally require a very unpleasant ealculation. So we might, for large $n$, turn to the eentral limit theorem, noting that
$$
k=x_{1}+x_{2}+\cdots+x_{n}
$$




傅立叶分析法|Fourier Analysis代写 6CCM318A

0
Posted on by

这是一份kcl伦敦大学学院  6CCM318A作业代写的成功案

傅立叶分析法|Fourier Analysis代写 6CCM318A
问题 1.

The general solution of $y^{\prime \prime}+\lambda y=0$ is
$y=A \cos \sqrt{\lambda} x+B \sin \sqrt{\lambda} x$
Then from the condition $y(0)=0$ we find $A=0$, so that
$$
y=B \sin \sqrt{\lambda} x
$$


证明 .

The condition $y^{\prime}(L)+\beta y(L)=0$ gives
$$
B \sqrt{\lambda} \cos \sqrt{\lambda} L+\beta B \sin \sqrt{\lambda} L=0{ }^{\prime} \quad \text { or } \quad \tan \sqrt{\lambda} L=-\frac{\sqrt{\lambda}}{\beta}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

6CCM318ACOURSE NOTES ：

$$
R=r^{-1 / 2}\left[A r \sqrt{1 / 4-\lambda^{2}}+B r^{\left.-\sqrt{1 / 4-\lambda^{2}}\right]}\right.
$$
or
$$
R=A r^{-1 / 2}+\sqrt{1 / 4-\lambda^{2}}+B r^{-1 / 2-\sqrt{1 / 4-\lambda^{2}}}
$$
This solution can be simplified if we write
$$
-\frac{1}{2}+\sqrt{\frac{1}{4}-\lambda^{2}}=n
$$
so that
$$
-\frac{1}{2}-\sqrt{\frac{1}{4}-\lambda^{2}}=-n-1
$$
In sueh case $(1)$ becomes
$$
R=A r^{n}+\frac{B}{r^{m+1}}
$$
Multiplying equations $(2)$ and $(s)$ together leads to
$$
\lambda^{2}=-n(n+1)
$$




复杂系统的平衡性分析|Equilibrium Analysis Of Complex Systems代写 7CCMCS03

0
Posted on by

这是一份kcl伦敦大学学院  7CCMCS03作业代写的成功案

复杂系统的平衡性分析|Equilibrium Analysis Of Complex Systems代写 7CCMCS03
问题 1.

This is now explicitly of a form that can be evaluated by the saddle point method. Note also, that results do not depend on the specific realization of the randomness, but only on the distributions of the random fields $h_{i}$ and the $\boldsymbol{\xi}{i}$ ! Fixed point equations are $$ \begin{aligned} \mathrm{i} \hat{m}{\boldsymbol{x}} &=\beta \sum_{\boldsymbol{x}^{\prime}} Q\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) p_{\boldsymbol{x}^{\prime}} m_{\boldsymbol{x}^{\prime}} \
m_{\boldsymbol{x}} &=\left\langle\tanh \left(\mathrm{i} \hat{m}{\boldsymbol{x}}+\beta h\right)\right\rangle{h}
\end{aligned}
$$


证明 .

Inserting the solution of the first into the second, we get
$$
m_{\boldsymbol{x}}=\left\langle\tanh \left[\beta \sum_{\boldsymbol{x}^{\prime}} Q\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) p_{\boldsymbol{x}^{\prime}} m_{\boldsymbol{x}^{\prime}}+\beta h\right]\right\rangle_{h},
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

7CCMCS03COURSE NOTES ：

$$
\Delta=\frac{1}{i \lambda_{\varepsilon}+J^{2} \Delta}
$$
This is a quadratic equation for $\Delta$, which is solved by
$$
\Delta_{1,2}=-\mathrm{i} \frac{\lambda_{\varepsilon}}{2 J^{2}} \pm \frac{1}{2 J^{2}} \sqrt{4 J^{2}-\lambda_{\varepsilon}^{2}}
$$
Taking the limit $\varepsilon \rightarrow 0$ we have
$$
\operatorname{Re} \Delta_{i}=\operatorname{Re} \Delta= \begin{cases}\frac{1}{2 J^{2}} \sqrt{4 J^{2}-\lambda^{2}} & ;|\lambda| \leq 2 J \ 0 & ;|\lambda|>2 J\end{cases}
$$
which when inserted into finally gives
$$
\rho(\lambda)=\frac{1}{2 \pi J^{2}} \sqrt{4 J^{2}-\lambda^{2}}, \quad|\lambda| \leq 2 J
$$




统计学习要素|Elements Of Statistical Learning代写  7CCMCS06

0
Posted on by

这是一份kcl伦敦大学学院  7CCMCS06作业代写的成功案

统计学习要素|Elements Of Statistical Learning代写  7CCMCS06
问题 1.

This expression shows that independent variables act multiplicatively on the baseline hazard, $\lambda_{0}$. With no loss of generality, the baseline hazard term $\left(\lambda_{0}\right)$ can be absorbed into the intercept term as
$$
\begin{aligned}
\lambda_{i} &=\exp \left(\sum_{k} \beta_{k} x_{i k}\right) \quad k=0, \ldots, K \
&=\exp \left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}\right),
\end{aligned}
$$


证明 .

When the independent variables are categorical (or can be treated as such), the data can be grouped as in Table 5.2. For a contingency table with $J$ cells, the data likelihood can be expressed in terms of the cell-specific occurrences $\left(D_{j}\right)$ and exposures $\left(E_{j}\right)(j=1, \ldots, J)$ as
$$
L=\prod_{j=1}^{J} \lambda_{j}^{D_{j}} \exp \left(-E_{j} \lambda_{j}\right)
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

 7CCMCS06 COURSE NOTES ：

$$
\mu_{i}=t_{i} \lambda_{i}=t_{i} \exp \left(\mathbf{x}{i}^{\prime} \boldsymbol{\beta}\right) . $$ The likelihood is a product of the individual Poisson probabilities in Eq. $5.11$ and is proportional to $$ L=\prod{i=1}^{n}\left(t_{i} \lambda_{i}\right)^{d_{i}} \exp \left(-t_{i} \lambda_{i}\right) .
$$
To show the equivalence between Poisson regression and the exponential rate model, note that exponential likelihood in Eq. $5.9$ can also be written as
$$
L=\prod_{i=1}^{n}\left(t_{i} \lambda_{i}\right)^{d_{i}} \exp \left(-t_{i} \lambda_{i}\right) / \prod_{i=1}^{n} t_{i}^{d_{i}}
$$




离散数学|Discrete Mathematics代写 5CCM251A

0
Posted on by

这是一份kcl伦敦大学学院 5CCM251A作业代写的成功案

离散数学|Discrete Mathematics代写 5CCM251A
问题 1.

3.8.2. We apply the lower bound in Lemma 2.5.1 to the logarithms. For a typical term, we get
$$
\ln \left(\frac{m+t-k}{m-k}\right) \geq \frac{\frac{m+t-k}{m-k}-1}{\frac{m+t-k}{m-k}}=\frac{t}{m+t-k}
$$


证明 .

and so
$$
\begin{aligned}
\ln \left(\frac{m+t}{m}\right) &+\ln \left(\frac{m+t-1}{m-1}\right)+\cdots+\ln \left(\frac{m+1}{m-t+1}\right) \
& \geq \frac{t}{m+t}+\frac{t}{m+t-1}+\cdots+\frac{t}{m+1}
\end{aligned}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

5CCM251A COURSE NOTES ：

For $n=1$ and $n=2$, if we require that $L_{n}$ be of the given form, then we get
$$
L_{1}=1=a+b, \quad L_{2}=3=a \frac{1+\sqrt{5}}{2}+b \frac{1-\sqrt{5}}{2}
$$
Solving for $a$ and $b$, we get
$$
a=\frac{1+\sqrt{5}}{2}, \quad b=\frac{1-\sqrt{5}}{2}
$$
Then
$$
L_{n}=\left(\frac{1+\sqrt{5}}{2}\right)^{n}+\left(\frac{1-\sqrt{5}}{2}\right)^{n}
$$